Mann-Whitney U toets
Contents
8. Mann-Whitney U toets#
8.1. Toepassing#
Gebruik de Mann-Whitney U toets om te toetsen of de gemiddelde rangnummers van de verdelingen van twee ongepaarde groepen van elkaar verschillen.1 De Mann-Whitney U toets is een alternatief voor de ongepaarde t-toets als de verdelingen niet normaal verdeeld zijn. Alleen als de verdelingen van beide groepen dezelfde vorm hebben, kan de Mann-Whitney U toets ook gebruikt worden om het verschil tussen de medianen van twee groepen te toetsen.9 Gebruik Mood’s mediaan toets om medianen te toetsen bij twee ongepaarde groepen waarvan de verdelingen niet dezelfde vorm hebben.
8.2. Onderwijscasus#
Dit onderzoek vertaalt zich in de volgende combinatie van hypothesen, waarbij de nulhypothese zo geformuleerd is dat er geen effect of verschil is en de alternatieve hypothese zo geformuleerd is dat er wel een effect of verschil is.
H0: Er is geen verschil in het gemiddelde rangnummer van het behaalde aantal studiepunten in het tweede jaar tussen studenten met een buitenlandse vooropleiding en een Nederlandse vooropleiding.
HA: Er is een verschil in gemiddelde rangnummer van het behaalde aantal studiepunten in het tweede jaar tussen studenten met een buitenlandse vooropleiding en een Nederlandse vooropleiding. Eén van beide verdelingen bevat hogere waarden betreffende het behaalde aantal studiepunten.
8.3. Assumpties#
Het meetniveau van de afhankelijke variabele is ordinaal12 of continu.9 In deze toetspagina staat een casus met continue data centraal; een casus met ordinale data met bijbehorende uitwerking is te vinden in de Mann-Whitney U toets II.
De Mann-Whitney U toets hoeft - in tegenstelling tot de ongepaarde t-toets - niet te voldoen aan de assumptie van normaliteit. Daarnaast hebben uitbijters minder invloed op het eindresultaat dan bij de ongepaarde t-toets. Daarentegen, als de data wel normaal verdeeld is, heeft de Mann-Whitney U toets minder onderscheidend vermogen2 dan de ongepaarde t-toets. Vandaar dat ondanks het voordeel van de grotere robuustheid er toch minder vaak voor de Mann-Whitney U toets gekozen wordt.
8.3.1. Verdeling steekproeven#
De Mann-Whitney U toets schrijft geen assumpties voor over de verdeling van de twee ongepaarde groepen.9 In principe toetst de Mann-Whitney U toets een hypothese over het verschil tussen het gemiddelde rangnummer van de verdelingen van twee ongepaarde groepen. De Mann-Whitney U toets maakt een rangschikking van alle observaties van beide groepen samengevoegd en telt vervolgens apart de rangnummers op voor de observaties in beide groepen. Met behulp van de groepsgroottes kan ook het gemiddelde rangnummer van beide groepen berekend worden. Het verschil tussen de gemiddelde rangnummers in beide groepen bepaalt de significantie van de toets.10 Daarom kan de Mann-Whitney U toets gezien worden als een toets die het gemiddelde rangnummer van twee groepen vergelijkt.
Als de verdelingen van de groepen niet dezelfde vorm hebben, doet de Mann-Whitney U toets een uitspraak over het verschil tussen verdelingen. Een verschil tussen verdelingen kan meerdere oorzaken hebben. De top of toppen van de verdelingen kunnen verschillend zijn, maar ook de spreiding van de verdeling kan verschillen.9 In alle gevallen is er echter een verschil tussen het gemiddelde rangnummer van de verdelingen. In andere woorden, de ene verdeling bevat hogere waarden dan de andere verdeling. Benoem daarom het gemiddelde rangnummer van beide groepen in de rapportage en visualiseer de verdeling van beide groepen om duidelijk te maken op welke manier de verdelingen van elkaar verschillen.
Als de verdelingen van beide ongepaarde groepen echter dezelfde vorm hebben, toetst de Mann-Whitney U toets ook een hypothese over het verschil tussen de medianen. Immers, het enige verschil tussen de verdeling is in dat geval een verschuiving van de verdeling, dus een verandering van de mediaan. In dat geval heeft de Mann-Whitney U toets een hoger onderscheidend vermogen2 dan Mood’s mediaan toets om medianen te toetsen.10
8.4. Effectmaat#
De p-waarde geeft aan of een (mogelijk) verschil tussen twee groepen significant is. De grootte van het verschil of effect is echter ook relevant. Een effectmaat is een gestandaardiseerde maat die de grootte van een effect weergeeft, zodat effecten van verschillende onderzoeken met elkaar vergeleken kunnen worden.3
De Mann-Whitney U toets heeft als effectmaat r. Een indicatie om r te interpreteren is: rond 0,1 is het een klein effect, rond 0,3 is het een gemiddeld effect en rond 0,5 is het een groot effect.5 De effectmaat r wordt voor de Mann-Whitney U toets berekend door de z-waarde behorend bij de p-waarde van de toets te delen door de wortel van het aantal observaties, i.e. \(\frac{z}{\sqrt{N}}\).5 Een correlatie tussen twee variabelen wordt vaak ook aangeduid met het symbool r. Beide zijn effectmaten, maar er is verder geen verband tussen de correlatie en de effectmaat van de Wilcoxon signed rank toets.
8.5. Uitvoering#
Er is data ingeladen met het aantal studiepunten dat studenten in het tweede jaar halen. dfPunten_jaar2_NL bevat Nederlandse studenten, dfPunten_jaar2_inter bevat internationale studenten.
8.5.1. De data bekijken#
Gebruik <dataframe>.head() en <dataframe>.tail() om de structuur van de data te bekijken.
# Pandas library importeren
import pandas as pd
## Eerste 6 observaties
print(dfStudiepunten_studiejaar2.head(6))
Studentnummer Studiepunten Vooropleiding
0 3000364 0 Nederlands
1 3000372 57 buitenlands
2 3000548 12 Nederlands
3 3000715 0 buitenlands
4 3000964 42 Nederlands
5 3001081 48 Nederlands
## Laatste 6 observaties
print(dfStudiepunten_studiejaar2.tail(6))
Studentnummer Studiepunten Vooropleiding
1494 3994944 48 Nederlands
1495 3995230 6 buitenlands
1496 3995911 51 Nederlands
1497 3996339 0 Nederlands
1498 3996684 57 buitenlands
1499 3997148 66 buitenlands
Bekijk de grootte, de mediaan en de kwantielen van de data met np.size() en np.quantile(). De mediaan en kwantielen worden vaak gebruikt als maat wanneer een verdeling niet symmetrisch is.
Studiepunten_Nederlands = dfStudiepunten_studiejaar2[
dfStudiepunten_studiejaar2["Vooropleiding"] == "Nederlands"]["Studiepunten"]
Studiepunten_buitenlands = dfStudiepunten_studiejaar2[
dfStudiepunten_studiejaar2["Vooropleiding"] == "buitenlands"]["Studiepunten"]
import numpy as np
print(np.size(Studiepunten_Nederlands))
print(np.quantile(Studiepunten_Nederlands, [0, 0.25, 0.5, 0.75, 1]))
950
[ 0. 6. 45. 57. 66.]
print(np.size(Studiepunten_buitenlands))
print(np.quantile(Studiepunten_buitenlands, [0, 0.25, 0.5, 0.75, 1]))
550
[ 0. 0. 12. 48. 66.]
vN_NL = len(Studiepunten_Nederlands) vN_Inter = len(Studiepunten_buitenlands)
vQ1_NL = q_NL[1] vQ1_Inter = q_Inter[1]
vQ2_NL = q_NL[2] vQ2_Inter = q_Inter[2]
vQ3_NL = q_NL[3] vQ3_Inter = q_Inter[3]
<!-- ## /CLOSEDBLOK: Data-beschrijven-3.py -->
<!-- ## TEKSTBLOK: Data-beschrijven2.py -->
* Mediaan studenten Nederlandse vooropleiding: `r Round_and_format(py$vQ2_NL)`, *n* = `r py$vN_NL`.
* Mediaan studenten buitenlandse vooropleiding: `r Round_and_format(py$vQ2_Inter)`, *n* = `r py$vN_Inter`.
<!-- ## /TEKSTBLOK: Data-beschrijven2.py -->
8.5.2. De data visualiseren#
Maak een histogram18 om de verdeling van het aantal studiepunten in het tweede jaar voor studenten met een Nederlandse en buitenlandse vooropleiding visueel weer te geven.13
## Histogram met matplotlib
import matplotlib.pyplot as plt
fig = plt.figure(figsize = (15, 10))
sub1 = fig.add_subplot(1, 2, 1)
title1 = plt.title("Nederlandse vooropleiding")
hist1 = plt.hist(Studiepunten_Nederlands, density = True, edgecolor = "black", bins = 29)
sub2 = fig.add_subplot(1, 2, 2)
title2 = plt.title("Buitenlandse vooropleiding")
hist2 = plt.hist(Studiepunten_buitenlands, density = True, edgecolor = "black", bins = 31)
main = fig.suptitle('Studiepunten van studenten Business Administration in het tweede jaar')
plt.show()
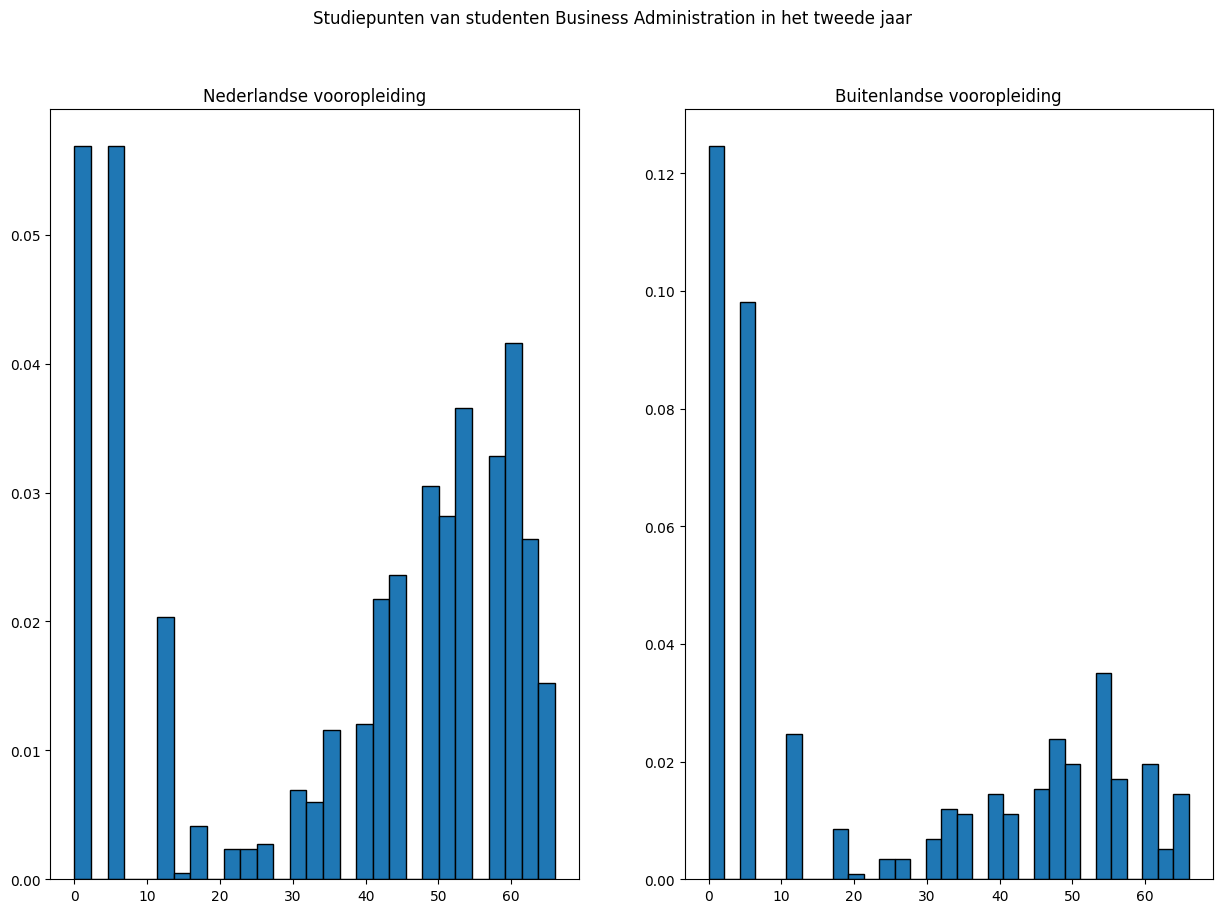
Beide histogrammen bevatten een grote groep studenten met een laag aantal studiepunten (twaalf of minder). De overige studenten volgen een ietwat scheve verdeling met de top rond de vijftig studiepunten. De verdelingen van beide groepen studenten hebben echter niet dezelfde vorm. De frequentie van het aantal studenten rond de vijftig studiepunten is veel hoger voor de studenten met Nederlandse vooropleiding, terwijl de frequentie van het aantal studenten met twaalf of minder studiepunten juist hoger is voor de studenten met een buitenlandse vooropleiding. De Mann-Whitney U toets kan in dit geval dus niet gebruikt worden om een uitspraak te doen over de significantie van het verschil van de medianen van beide groepen.
8.5.3. Mann-Whitney U toets#
Gebruik de functie mannwhitneyu() van het scipy package om een Mann-Whitney U toets te doen. Het eerste argument bevat het aantal studiepunten van studenten met een Nederlandse vooropleiding Studiepunten_Nederlands; het tweede argument het aantal studiepunten van studenten met een buitenlandse vooropleiding Studiepunten_buitenlands. Voer daarna het argument alternative = 'two-sided' vanwege de tweezijdige alternatieve hypothese.
import scipy.stats as sp
sp.mannwhitneyu(Studiepunten_Nederlands,
Studiepunten_buitenlands,
alternative = 'two-sided')
MannwhitneyuResult(statistic=336533.5, pvalue=7.419881960900597e-21)
Bereken vervolgens de effectmaat r op basis van de p-waarde van de Mann-Whitney U toets.
df = pd.read_csv("../data/07_Alumni_jaarinkomens.csv")
dfAlumni_jaarinkomens = df.loc[:, ~df.columns.str.contains('^Unnamed')]
Alumni_jaarinkomens_T1 = dfAlumni_jaarinkomens[dfAlumni_jaarinkomens["Meetmoment"] == "T1"]["Inkomen"]
Alumni_jaarinkomens_T2 = dfAlumni_jaarinkomens[dfAlumni_jaarinkomens["Meetmoment"] == "T2"]["Inkomen"]
# Sla de p-waarde op
stat, pval = sp.wilcoxon(Alumni_jaarinkomens_T2, Alumni_jaarinkomens_T1, alternative = 'two-sided')
# Bereken de effectgrootte voor een tweezijdige toets
Effectmaat = sp.norm.ppf(pval/2) / np.sqrt(len(Alumni_jaarinkomens_T1))
# Bereken de effectgrootte voor een eenzijdige toets
#r = sp.norm.ppf(pval) / np.sqrt(len(Alumni_jaarinkomens_T1))
# Print de effectgrootte (vaak weergegeven als absolute waarde)
print(np.abs(Effectmaat))
1.0108893680167252
Bereken ten slotte het gemiddelde rangnummer van beide groepen. Beoordeel op basis van de gemiddelde rangnummers welke groep hogere waardes bevat.
#dfStudiepunten_studiejaar2[dfStudiepunten_studiejaar2["Vooropleiding"] == "Nederlands"]["Studiepunten"]
vvv = dfStudiepunten_studiejaar2["Vooropleiding"] == "Nederlands"
print(vvv)
dfStudiepunten_studiejaar2[-vvv]
0 True
1 False
2 True
3 False
4 True
...
1495 False
1496 True
1497 True
1498 False
1499 False
Name: Vooropleiding, Length: 1500, dtype: bool
| Studentnummer | Studiepunten | Vooropleiding | |
|---|---|---|---|
| 1 | 3000372 | 57 | buitenlands |
| 3 | 3000715 | 0 | buitenlands |
| 6 | 3001192 | 0 | buitenlands |
| 7 | 3001803 | 0 | buitenlands |
| 8 | 3002896 | 12 | buitenlands |
| ... | ... | ... | ... |
| 1491 | 3993012 | 54 | buitenlands |
| 1493 | 3994496 | 6 | buitenlands |
| 1495 | 3995230 | 6 | buitenlands |
| 1498 | 3996684 | 57 | buitenlands |
| 1499 | 3997148 | 66 | buitenlands |
550 rows × 3 columns
# Sla de studiepunten variabele op in vector
Studiepunten_vector = dfStudiepunten_studiejaar2["Studiepunten"]
# Rangschik de studiepunten
Rangnummers = sp.rankdata(dfStudiepunten_studiejaar2["Studiepunten"])
# Bepaal de index met daarin studenten met een Nederlandse vooropleiding
Vooropleiding_Nederlands = dfStudiepunten_studiejaar2["Vooropleiding"] == "Nederlands"
# Bereken gemiddelde rangnummers
N_positief = len(Studiepunten_vector[Vooropleiding_Nederlands == True])
print(N_positief)
Rangnummer_Nederlandse_vooropleiding = np.sum(Rangnummers[Vooropleiding_Nederlands == True]) / N_positief
N_negatief = len(Studiepunten_vector[Vooropleiding_Nederlands == False])
print(N_positief)
Rangnummer_buitenlandse_vooropleiding = np.sum(Rangnummers[Vooropleiding_Nederlands == False]) / N_negatief
# Print gemiddelde rangnummers
print(Rangnummer_Nederlandse_vooropleiding)
print(Rangnummer_buitenlandse_vooropleiding)
950
950
829.7457894736842
613.6209090909091
W =
r Round_and_format(py$stat), p = < 0,0001, r =r Round_and_format(abs(py$Effectmaat))p-waarde < 0,05, dus de H0 wordt verworpen.8
Effectmaat is
r Round_and_format(abs(py$Effectmaat)), dus een klein tot gemiddeld effectHet gemiddelde rangnummer is
r Round_and_format(py$Rangnummer_Nederlandse_vooropleiding)(n=r py$N_positief) voor studenten met een Nederlandse vooropleiding enr Round_and_format(py$Rangnummer_buitenlandse_vooropleiding)(n=r py$N_negatief) voor studenten met een buitenlandse vooropleiding. De verdeling van studenten met een Nederlandse vooropleiding bevat dus hogere waarden dan de verdeling van studenten met een buitenlandse vooropleiding.
8.6. Rapportage#
De Mann-Whitney U toets is uitgevoerd om te toetsen of het behaalde aantal studiepunten in het tweede jaar van de bachelor Business Administration hetzelfde is voor studenten met buitenlandse vooropleiding als voor studenten met Nederlandse vooropleiding. Uit de resultaten kan afgelezen worden dat er een significant verschil is tussen de verdelingen van het aantal studiepunten van studenten met een buitenlandse vooropleiding en met een Nederlandse vooropleiding, W = r Round_and_format(py$stat), p < 0,0001, r = r Round_and_format(abs(py$Effectmaat)). Er is een klein tot gemiddeld effect van het verschil in het land van vooropleiding op het aantal studiepunten. Het gemiddelde rangnummer is r Round_and_format(py$Rangnummer_Nederlandse_vooropleiding) (n=r py$N_positief) voor studenten met een Nederlandse vooropleiding en r Round_and_format(py$Rangnummer_buitenlandse_vooropleiding) (n=r py$N_negatief) voor studenten met een buitenlandse vooropleiding. Studenten met een Nederlandse vooropleiding lijken dus een hoger aantal studiepunten te halen in het tweede jaar dan studenten met een buitenlandse vooropleiding.
- 1
Van Geloven, N. (13 maart 2018). Mann-Whitney U toets. Wiki Statistiek Academisch Medisch Centrum.
- 9(1,2,3,4)
Laerd Statistics (2018). Mann-Whitney U Test using SPSS Statistics. https://statistics.laerd.com/spss-tutorials/mann-whitney-u-test-using-spss-statistics.php
- 12
Een ordinale variabele is een categorische variabele waarbij de categorieën geordend kunnen worden. Een voorbeeld is de variabele beoordeling met de categorieën Onvoldoende, Voldoende, Goed en Uitstekend.
- 2(1,2)
Onderscheidend vermogen, in het Engels power genoemd, is de kans dat de nulhypothese verworpen wordt wanneer de alternatieve hypothese ‘waar’ is.
- 10(1,2)
Field, A. (2013). Discovering statistics using IBM SPSS statistics. Sage.
- 3
Field, A., Miles, J., & Field, Z. (2012). Discovering statistics using R. London: Sage publications.
- 5(1,2)
Allen, P. & Bennett, K. (2012). SPSS A practical Guide version 20.0. Cengage Learning Australia Pty Limited.
- 18
De breedte van de staven van het histogram wordt vaak automatisch bepaald, maar kan handmatig aangepast worden. Aangezien de breedte van de staven bepalend zijn voor de indruk die de visualisatie geeft, is het verstandig om hier goed op te letten.
- 13
De breedte van de staven van het histogram worden hier automatisch bepaald, maar kunnen handmatig aangepast worden. Aangezien de breedte van de staven bepalend zijn voor de indruk die de visualisatie geeft, is het verstandig om hier goed op te letten.
- 8
In dit voorbeeld wordt uitgegaan van een waarschijnlijkheid van 95% c.q. een p-waardegrens van 0,05. De grens is naar eigen inzicht aan te passen; houd hierbij rekening met type I en type II fouten.

